Bugün erken saatlerde size kitaptan bu sorunları anlattım. Matematik Problemlerine Yanal Çözümler Des MacHale tarafından. Cevaplarla yine karşınızdayız.
1. Bir portakalın üstüne üç karanfil
Bir kürenin yüzeyindeki üç nokta göz önüne alındığında, bunların hepsinin üzerinde bulunduğu bir yarımkürenin bulunma olasılığı nedir?
Cevap Yüzde 100
Herhangi bir hesaplama yapmayın. Şöyle düşünün: Kürenin yüzeyine rastgele iki nokta koyun (yani bir portakalın üzerine rastgele iki karanfil yerleştirin). Şimdi küreyi (turuncuyu) bu iki noktadan (karanfillerden) geçecek şekilde ikiye bölün. Artık iki yarımküreniz var ve bunların her ikisi de iki noktayı içeriyor. Üçüncü rastgele nokta (veya karanfil) bu yarım kürelerden birinde olacaktır.
2. Büyük bir sayı
Bir milyondan küçük tüm asal sayıları toplarsanız cevabın son rakamı kaç olur?
(Asal sayı, yalnızca kendisine ve 1’e bölünebilen bir sayıdır; örneğin 2, 3, 5, 7, 11, 13 vb.)
Cevap: Sayı 0 ile bitecek.
Tekrar ediyorum, hepsini çarpmayı aklınızdan bile geçirmeyin. Sayı 2 x 3 x 5 x 7 x….
2 x 5 = 10 olduğuna göre bunu 10 x 3 x 7 x… şeklinde yeniden yazabiliriz.
10’un katı olan her tam sayının sonu 0’dır.
3. Üç üçlü
Üç üçlüyü ve istediğiniz herhangi bir matematik işlemini kullanarak 20 yapabilir misiniz?
(yani 3, 3 ve 3’ü içeren ve başka rakam içermeyen ancak +, -, x, ÷, (, ), √, ., vb. gibi başka herhangi bir matematik sembolünü içerebilen bir ifade bulmanız gerekir. örnek 3 olabilir√3/3, ancak 20’ye eşit olmadığı için bu yanlış olur.)
Cevap
İşin püf noktası ondalık nokta kullanmaktır. İşte bir yol:
20 = (3 + 3)/.3
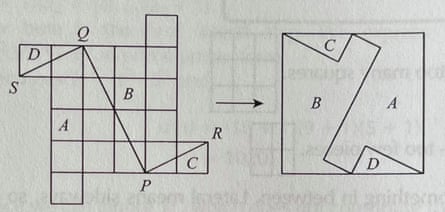
4. Kare misin?
Bu şekli bir kare oluşturacak şekilde yeniden birleştirilebilecek dört parçaya nasıl kesebilirsiniz?
Çözüm
Şekilde 20 adet küçük kare bulunmaktadır. Yani eğer bunlar büyük bir kare oluşturacak şekilde bir araya getirilecekse, bu büyük karenin bir kenarının √20 olması gerekir. Diyagramda √20 uzunluğunda bir doğru bulmaya çalışalım.
Dik açılı üçgenler için Pisagor Teoremi, hipotenüsün karesinin diğer iki kenarın karelerinin toplamına eşit olduğunu belirtir. 2’den beri2 + 42 = 20 = (√20)2 Kenarları 2 ve 4 kısa olan dik açılı bir üçgenin hipotenüsünün bize gerekli uzunluğu sağlayacağını biliyoruz. Dolayısıyla aşağıdaki resimde PQ’nun uzunluğu √20’dir. Bir kare yaptığımıza göre, bir başka iyi bahis de P ve Q’daki kesimin 90 dereceye doğru gitmesidir. Ve işte.
5. Dolaşım rakamları
Tam olarak hareket ederek denklemi geçerli hale getirin iki kibrit çöpleri
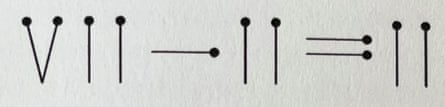
Cevap İşte bir yol.
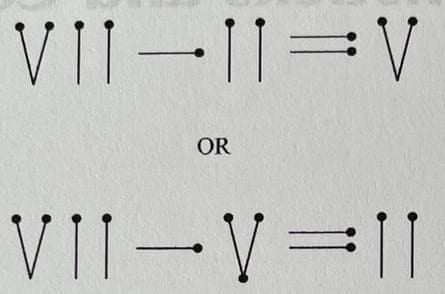
Ve işte bir tane daha:
Başka bir tane bulursanız, lütfen satırın altında bana bildirin!
Tamamı mükemmel yeni kitabından alınan bugünkü bulmacalar için Des MacHale’e teşekkürler. Matematik Problemlerine Yanal Çözümler.
2015’ten bu yana dönüşümlü olarak Pazartesi günleri burada bulmaca hazırlıyorum. Her zaman harika bulmacalar arayışındayım. Bir tane önermek isterseniz bana e-posta gönderin.

